Polisiyenin bilimle ilişkisini ele aldığımız 6. sayımızda Yunan matematikçi ve yazar Tefkros Mihalidis, polisiye kurguda matematiğin yerini anlatıyordu. Mihalidis, “Matematiğin polisiye edebiyatla etkileşimi Poe ve Doyle gibi yazarların öncülüğünde başlamıştır. Bugün artık, polisiye edebiyatla matematiksel kurgu, kural gereği, birbirlerine iyi ya da kötü etki eden iki edebiyat türü olarak karşımızdadır,” diyor…
Her edebi eser, hangi kategoriye girerse girsin (eğer giriyorsa), gerçek hayattan bir fotoğrafı (ya da en azından bir taslağı) andırır. Ancak kural gereği, bilimler resmedilen dünyanın alt dalları olsa da kurgunun bilimlere doğrudan başvurmadan gelişmesi gerekir. Örneğin, duygusal bir öykünün, psikolojik ya da toplumsal bir dramın, bir arayış öyküsünün ya da bir tarihi romanın kimya, fizik, biyoloji ya da tıbba atıfta bulunma gibi bir zorunluluğu asla yoktur.
Ancak polisiye edebiyat için bu geçerli olmayabilir. Elbette teknoloji geliştikçe, suçun kurgunun merkezinde bulunduğu eserlerde bir pozitif bilimden yararlanmak ya da en azından onu suiistimal etmek gerekir. Belki de polisiye edebiyat (ya da cinayet kurgusu veya Anglosakson terimiyle crime friction türü), diğer edebiyat türlerine göre biraz farklıdır. Pek çok uzmana göre, polisiye edebiyat 19. yüzyıl başlarında, daha spesifik olarak 1841 yılında, Poe’nun Morg Sokağı Cinayetleri adlı öyküyü Graham’s Magazine’de yayımlamasıyla başlamıştır. Esasen, böylesi bir edebi türün sanayi devriminin geliştiği ve buna bağlı olarak pozitif bilimlerin hüküm sürdüğü bir dönemde ortaya çıkması rastlantı değildir. Net bir biçimde, pozitif bilimlerden etkilenme sözkonusudur.
Polisiye öyküde bilimselliğin rolü
Öte yandan, belki daha da önemlisi, polisiye edebiyatta kurgu büyük ölçüde doğal olguların (ölüm katılaşması, renk değişimi, zehirli maddelerin kullanımı, mermi yörüngesi, ses ve ışık yayılması vb.) pozitif bilimlere dayanmaması mümkün değildir. Yazar, bir cinayetin işlenişini, saklanışını ya da aydınlatılmasını tasvir etmek için pozitif bilimlere az ya da çok dayanmak zorundadır. Bu türden öykülerde, gerçekçilik neredeyse her zaman aranan bir özelliktir. Bir polisiye öyküdeki bilimsellik bir bilimkurgudakinden çok daha önemlidir. Zamanda yolculuk, geçmişe ya da geleceğe gidiş ya da otomatik iradeyle hareket eden bir makine, elbette bilimdışı olabilir. Ancak bir kurbanın ölüm saatinin saptanması, bir kan damlasından ya da saç telinden kimlik tespiti yapılması veya zehirli bir maddenin açığa çıkarılmasında genellikle bilimdışılık olmaz.
90’lara kadar, polisiye edebiyattan uzak kalan tek pozitif bilim, matematikti. Aralarında gözle görünür bir mesafe vardı. Edgar Allan Poe, polisiye öyküleri, özellikle hipotez sürecini matematikselleştiren Gottfried Wilhelm von Leibiz’in sevdiği bir terim olan “rasyonel öyküler” (tales of ratiocination) terimini kullanarak tanımlamaktadır. Fakat polisiye edebiyatın öncüsünün matematikle ilişkisi burada başlayıp bitiyor.
Benzer bir şey, ortaya çıkışının ilk yüzyılında polisiye edebiyata hizmet eden hemen herkes için geçerlidir. Matematiğe başvuran polisiye öykü yazarları, kurgularında kaynağını bu bilim dalından alan ya da bir şekilde yolu onunla kesişen kurgular oluşturma gayretinde bulunuyorlar. Sherlock Holmes’ün yöntemlerinin saygıdeğer olduğunu vurgulamak için, Arthur Conan Doyle, Watson’ı konuşturuyor: Onun (Holmes) sonuçları Öklid misali tartışılmaz, şüphe kaldırmazdı. 1
Başka bir eserde, yöntemlerinin nesnelliğinin altını çizmek için bizzat Sherlock Holmes, yardımcısını eleştirirken şöyle diyordu: Cinayeti çözmek, bir tür pozitif bilimdir ya da öyle olması gerekir. Cinayeti çözerken bir pozitif bilimde olduğu gibi soğukkanlı ve tamamen yansız davranmak gerekir. Sen işe romantizm katmaya çalışıyorsun. Bu ancak aşk öykülerinde olur. Bunun bir aşk öyküsü olduğunu zannetmekle Öklid kurallarının beşincisini göz ardı etmek arasında bir fark yoktur. Her ikisi de bize aynı sonucu aldırır. 2
Matematiksel düzen, kurgularını matematikten yararlanarak gerçek yaşama özgü araştırmalarla zenginleştiren yazarların diğer bir ortak özelliğidir:
– Bekas, burada üçüncü bir rakibin olması gerektiğini söyledi. Bu denklemi çözmez. Denklemi kırar […] Bana kalırsa, “üçüncü rakip” hipotezi problemi hem zorlaştırır hem de sıradanlaştırır. Bilinenlerden yola çıkarak bilinmeyenlere erişebiliriz.
Albay gülümsedi.
– Sevgili Bekas, matematikte zayıflıklarınız var. Sadece…
– Sadece?
– Sadece matematik, pozitif bilimlerin temel prensibini oluşturabilir. Oysa siz fantezi dünyanıza önemli bir rol biçmiş durumdasınız. 3
Metodoloji ve ontoloji, matematiksel karakteri olan kurgularda yazarların sıklıkla başvurduğu diğer unsurlardır. Auguste Dupin metodunu şöyle açıklamaktadır: Tesadüfleri bile sıkı ve nesnel hesaplarla açıklarız. Okulda matematik, araştırılamayanı ve düşünülemeyeni çözmekte bize yardımcı olur. 4
Arthur Conan Doyle da, Sherlock Holmes’ün en ilginç rakibi olan nevi şahsına münhasır Dr. Moriarty’yi bir matematik dehası olarak yaratıyor.
Polisiyenin matematik ve kanıtla ilişkisi
Diğer bir ilginç husus, matematik (ya da matematiğin eğitimi, popüler hale gelmesi) polisiye kurgu içerisinde bir sıra bütünlüğü şeklinde gelişmektedir. Yüzlerce matematik kitabında, “Bir matematik problemini çözmek, bir cinayetteki gizemi çözmek gibidir,” şeklindeki klişelere yer verilir. Pek çok matematik kitabı da başlığında dedektif, gizem ve serüven gibi ifadelere yer verir. Ancak matematikle polisiye kurgu arasında yukarıda tasvir ettiğimiz köprüler net biçimde yüzeyseldir, çünkü aralarındaki bağlantı farklı unsurların aynı sihirli kavram çerçevesinde birleştirilmesi sözkonusudur. Bu sihirli kavramın tek bir adı var: Kanıt.
Burada altını en başından net olarak çizmeliyiz ki matematikteki kanıt, hukuki bir süreçteki kanıttan köklü biçimde farklıdır. Bunun gerçek bir hukuki süreç ya da bir polisiye serüven kurgusu olması fark etmez. Her iki tip kanıt da insan ürünüdür. İyon filozoflarının döneminde, matematiksel bir gerçek, pazardan örneklere dayanarak sağlama yapmaya açık olabilen bir gerçekti. Günümüzdeyse pazarın rolünden örnekler vermek kriz hakkında yayın yapan dergilere ve akademisyenlere düşmektedir. Benzer bir şey hukuki kanıtlar için de geçerli. Kaza mahkemelerinde ya da yüksek idari mahkemelerde görüşülen davalardaki kanıt, dava hakkında son karar verilene kadar geçen süre içinde toplanır.
İşte tam da burada, iki kanıt arasındaki farklılık belirginleşir: Bir mahkeme kararı çoğunluk esasıyla, çoğu zaman mahkemeler, hukukçular ve yeminli vatandaşlar tarafından, toplumun genelini temsil etmek üzere neredeyse rastgele seçilen bireyler tarafından verilir. Avukatlar, elbette mahkemenin sentezini değerlendirir ve buna itirazları varsa, kararın makul olmadığını iddia ederlerse, farklı hukuki mekanizmalardan yararlanarak kararı değiştirebilirler. Fakat matematiksel bir kanıt üzerinde bu tür tartışmalar olamaz. Matematiksel kanıt oyçokluğuyla değil, oybirliğiyle yürür. Yeterli bilgiye sahip olan herkes, bir matematiksel kanıtı her an test edebilir. Nadiren, bilim dünyasında bazı matematiksel kanıtlar hatalı bulunabilir, ancak bu kanıtların hatalı olduğu üzerinde de oybirliği gerekir.
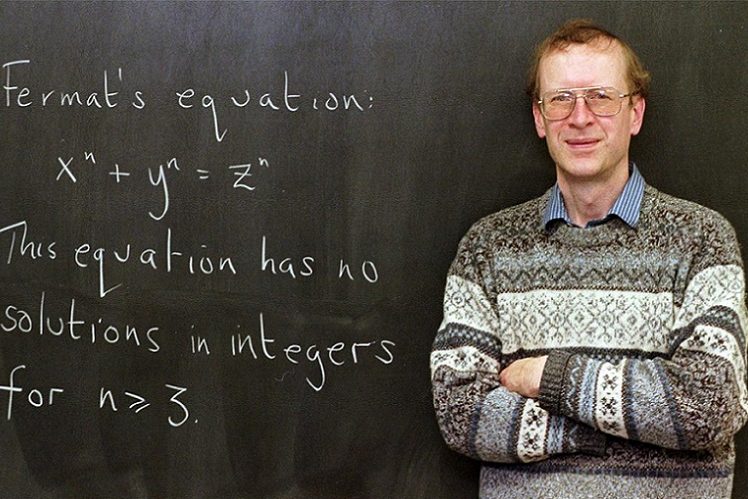
Matematiksel bir kanıtın çürütülmesi çok rastlanan bir şey değildir, ancak bunun örnekleri de mevcuttur. 1637 yılında, çiçeği burnunda matematikçi Pierre Fermat (ilginç olan Fermat’ın esasen hukukçu olmasıydı), şu şekilde bir formül geliştirmişti: “Eğer n ikiden büyük bir tamsayıysa ve x, y, z sayıları pozitif tamsayılarsa Xn+Yn=Zn olur.” 1992 yılında, Cambridge Üniversitesi’nde Andrew Wiles, Fermat’ın teoremini kanıtladığını açıkladığı zaman, bilim dünyası bunu sevinçle karşılamıştı. Fakat Wiles’ın bulduğu kanıt hatalıydı ve bunu derhal kendisi de kabul etmişti. Wiles teoremi, kanıtlananlar kategorisine ekleyecek kanıtı, ancak 3 yıl sonra bulabilecekti.
1852 yılında da Francis Guthrie, “Eğer her ülkenin tek bölgeden oluştuğu varsayılırsa bir siyasi haritanın tüm ülkeleri, komşu ülkeler aynı renge boyanmadan dört renge boyanabilir,” şeklindeki teoremi geliştirmişti. Problem, başlangıçta göründüğünden çok daha zordu. Nihayet 27 yıl sonra Alfred Bray Kempe, 1879 yılında matematik dünyasının doğru kabul ettiği bir kanıt sundu. Ancak bu kanıtta ayırt edilmesi zor bir hata vardı ve bu hata 11 yıl sonra Percy Heawood tarafından açığa çıkarılmıştı. Heawood’un tespiti, oyçokluğuyla kabul gördü ve konu üzerindeki tartışmalar yeniden başladı. Kenneth Appel ve Wolfgang Haken, 1976 yılında bir kanıt sundular. Ancak hikâye burada da bitmedi. Appel ve Haken, el yordamı ile değil, bilgisayar kullanarak çalışmıştı. Bu sefer de böylesi bir matematik probleminin çözümünde bilgisayardan yararlanmanın adil olup olmadığı tartışıldı. Bu probleme ilişkin olarak, bilim dünyası bugün bile bölünmüş durumdadır.
Matematik tarihinde hangi yöntemlerin kabul görüp görmeyeceği sıklıkla tartışılmış bir husustur. Proklos, Öklid’in Elementler kitabının ilk cildinde, eski çağlarda yaşayan pek çok matematikçinin olmayana ergi kullanımını kabul etmediklerini ifade etmektedir. 5 Ancak kanıta dayalı bu yöntem bugün evrensel düzeyde kabul görmektedir. Buna benzer anlaşmazlıklar varlık kanıtları açısından da mevcuttur. 20. yüzyıl başlarında, sezgicilik ekolü matematiksel bir nesnenin varlık kanıtının, üretim sürecinde sonsuz olmayan sayıda adımı içermesi gerektiğini kabul ediyordu. Böyle bir şey, pek çok matematiksel kanıtı geçersiz kılabilirdi. Ancak bu endişeler bugün aşılmış durumdadır.
Sayıları az olan, kanıta dayalı yöntemlerle ilgili oybirliği sağlanmış bu örnekler matematik ve hukuktaki kanıt kültürü açısından bazı benzerlikler göstermektedir ve bu zamandan ve şartlardan bağımsız değildir. Örneğin, baskı ya da işkence altında verilen ifadeler bugün kabul edilmez olarak değerlendirilirken, Ortaçağ’da hem Doğu’da hem Batı’da birer rutin halindeydiler. O çağlara değinen pek çok polisiye eser, bu türden kanıtlara sıklıkla değinmektedir. Robert van Gulik, Yargıç Dee’nin öykülerinde gizemleri aydınlatan kahraman bu tür yöntemlere başvurmaktan kaçınsa da bu tür yöntemlerle toplanan deliller de eksik olmazdı.
Tartışılan kanıtlar arasında, ses ve görüntü kayıtlarından oluşan ve hem ülkeden ülkeye, hem zamandan zamana farklılık gösteren kanıtlar da vardır. Hukuki kanıtla matematiksel kanıt bir açıdan birbirleriyle akrabadır ancak aralarındaki farklılıklar, benzerliklerden fazladır.
Matematiksel kanıtta sapma yoktur. Bir kanıt, ortaya konmasının ardından yüzlerce yıl geçse bile hatalı olduğu ispatlanırsa bütün hükmünü kaybeder. Mahkeme kanıtlarında böyle bir şey sözkonusu değildir. Mesela, İngiliz hukukunda bir suçlamadan beraat eden bir şahıs hakkında aynı suçlamayla ilgili yeniden dava açılamaz. Agatha Christie’nin ilk polisiye romanı Ölüm Sessiz Geldi, bu doğrultuda kurgulanıyor. Katil Alfred Inglethorp, yanlış veriler doğrultusunda yargıya taşınmaya çalışılıyor. Ortaya konan iddia çöküyor. Suçluluğunu ortaya koyan unsurlar daha sonra ortaya çıksa da katil tekrar yargılanamıyor.
Matematiksel kanıtla hukuki kanıt arasındaki bir diğer fark, matematikte bir kanıtın yakalanmasının genellikle farklı kesimlerde çıkar çatışması yaratmamasıdır. Maksat, kanıtın bulunması ve gerçeğin açığa çıkarılmasıdır. Ancak mahkeme süreçlerinde çıkar çatışmaları da net olarak yaşanır. Bir taraf bir şey savunurken diğer taraf başka bir şey savunur ve her ikisi de haklı çıkmaya çalışır. Burada bir fark daha vurgulanmalıdır; matematikte kanıtlar derecelere ayrılmaz, ancak hukukta ayrılır. Matematikte “birincil derece kanıt”, “ikincil derece kanıt” diye bir şey sözkonusu değilken bunlar hukukta mevcuttur. Hukukta bazı kanıtlar diğerlerinden daha önemli sayılır.
Yine göz önünde bulundurmak gerekir ki, bir matematiksel kanıtta, başlangıç varsayımının doğrulanması da çürütülmesi de aynı memnuniyeti yaratır. Her iki durumda da açık problemler kataloğuna eklenecek kayda değer bir sonuç çıkmış olur. Kısacası, şunu söyleyebiliriz: Mahkemelerdeki kanıtlar ve sonuçlar herkes için aynı derecede memnun edici olmaz.
Polisiye edebiyatla matematiksel kurgu, birbirini etkiler
90’ların başlarına kadar, matematik ve polisiye kurgu, aynı terimleri farklı anlamlarda ve içeriklerde kullandılar. 1998’de Denis Guedj’in Papağan Teoremi kitabı ve 2000’de İngilizceye çevrilen Petros Amca ve Goldbach Varsayımı isimli romanı, yeni bir kurgu türünün doğuşunun habercisi olmuştu. Pek çok kişi bu yeni türe matematiksel edebiyat adını vermişti.
Matematiksel edebiyat, matematikle polisiye edebiyat arasındaki ilişkilerin gelişmesi neticesinde ortaya çıktı. Papağan Teoremi, bir polisiye roman şeklinde yazılmıştı. Cinayet, insan kaçırma, kundaklama ve takip vardı. Polisin rolüyse, matematiksel bir öykü olarak kurgulanan karelerde taşların yerine oturmasını sağlamaktı.
Matematik ve polisiye edebiyatın çok daha özlü biçimde bir arada bulunduğu örnekler de mevcuttur. Bu genellikle yazarın, matematiği, kurgusundaki gizem unsurunun önemli bir parçası haline getirmesiyle olur. Böylece matematik, roman içerisinde daha da ilgi uyandıran bir öğe halini alır. Örneğin, Mark Cohen’in Fractal Murders isimli romanında, fraktal teoriyi ekonomide kullanan bir teoremin, üç cinayetin sebebiyle önemli bir bağlantısı vardı. Argiris Pavliotis’in Yasaklı Problem isimli romanında cinayetin sebebi ünlü bir matematik formülünü çözme hırsıyken, yazarın Pisagor Cinayetleri isimli romandaki cinayet sebebi ise evrendeki uyumun bir matematiksel kanıt tarafından bozulma tehlikesine dair gelişen bir paranoyadır.
Matematikle polisiye edebiyatın bağlarının daha da sıkı örüldüğü örnekler de vardır. Oxford Cinayetleri bunun önde gelen örnekleri arasındadır. Bu romanda matematik sadece olayların gelişimiyle değil, bir matematikçinin katili saklama çabalarıyla da alakalıdır. Bir matematikçi tarafından kollanan diğer bir katile ise Keigo Higashino’nun The Devotion of Suspect X isimli romanında rastlıyoruz. Bu romanın merkez kişisi, katili bilimden yararlanarak gizlemeye çalışan bir matematikçidir. Yazarın diğer romanında ise, Pisagor’un dost sayıları cinayetin aydınlatılmasında kilit rol oynuyor.
Cinayetin bir matematikçi yardımıyla aydınlatılması da romanlarda rastlanabilen bir durumdur. Bunun tipik örnekleri arasında Argiris Pavliotis’in Tuhaf Çekiciler romanı ve ünlü televizyon dizisi Sayılar da (Numbers) yer almaktadır.
Sonuç olarak, matematiğin polisiye edebiyatla etkileşimi Edgar Allan Poe ve Arthur Conan Doyle gibi yazarların öncülüğünde başlamış, bu yol arkadaşlığı 20 ve 21. yüzyıllarda daha da yakın bir ilişki çerçevesinde devam etmiştir. Bugün artık, polisiye edebiyatla matematiksel kurgu, kural gereği, birbirlerine iyi ya da kötü etki eden iki edebiyat türü olarak karşımızdadır.
Çeviri: Şevki Kıralp
Kaynakça
1- Arthur Conan Doyle: A Study In Scarlet.
2- Sherlock Holmes: The Sign of the Four.
3- Yannis Maris: Geçmişten bir kadın.
4- Edgar Allan Poe: The Mystery Of Marie Rogêt.
5- “…onu zayıf tarafından yakaladılar…”, Proklos, Öklid, Elementler Cilt I, ed. Friedlein, 73.20-25.
